Hogyan lehet megtalálni a parabola?

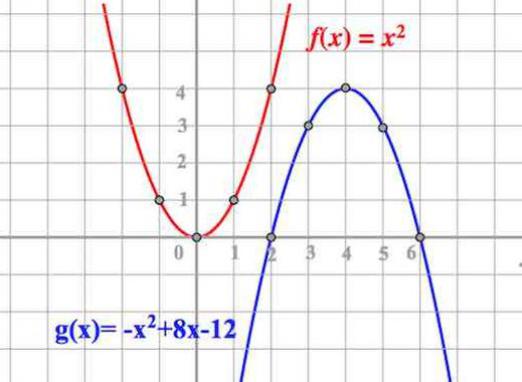
A parabola egy négyzetes függvény grafikonja. Ez a vonal jelentős fizikai jelentéssel bír. Annak érdekében, hogy könnyebb megtalálni a parabola csúcsát, meg kell rajzolnia. Ezután a térképen könnyen láthatja a tetejét. De egy parabola felépítéséhez meg kell tudni, hogyan lehet megtalálni a parabola pontokat, és hogyan lehet megtalálni a parabola koordinátáit.

Megtaláljuk a parabola pontját és csúcsát

Az általános ábrázolásban a kvadratikus függvénynek a következő alakja van: y = ax²+ bx + c. Ennek az egyenletnek a grafikonja egy parabola. Ha a> 0, az ágak felfelé irányulnak, és <0 - lefelé. A parabola grafikonon történő megépítéséhez három pontot kell tudni, ha az az ordinát tengelyen halad. Ellenkező esetben négy építési pontot kell ismerni.

Az abszcissza (x) megkeresésekor az adott polinom képletből kell venni az (x) együtthatót, majd az (x²), majd szorozzuk meg egy számmal - 1.

Az ordinátum megtalálásához meg kell találni a diszkriminanst, majd szorozzuk meg azt - 1-gyel, majd oszd meg az (x²), először 4-tel szorozva.

Továbbá, számszerű értékek helyettesítésével kiszámítjukparabola csúcsát. Minden számításhoz kívánatos egy mérnöki kalkulátort használni, és ha rajzokat és parabolokat rajzolunk egy vonalzó és egy lumo-grafikon használatára, ez jelentősen javítja a számítások pontosságát.

Tekintsük a következő példát, amely segít megérteni, hogyan lehet megtalálni a parabola csúcsát.

x²-9 = 0. Ebben az esetben a csúcs koordinátáit az alábbiak szerint kell kiszámítani: 1. pont (-0 / (2 * 1), 2. pont - (0 ^ 2-4 * 1 * (-9)) / (4 * 1)). Így a csúcs koordinátái az értékek (0; 9).

Keresse meg a csúcs abszcisszáját

Miután megtanulta, hogyan találja meg a parabolát, és kiszámíthatja annak metszéspontját a koordináta tengelyével (x), könnyen kiszámíthatja a csúcs abszcisszáját.

Tegyük fel, hogy (x₁) és (x₂) egy parabola gyökerei. A parabola gyökerei az abszcissza tengelye metszéspontjának pontjai. Ezek az értékek a következő alakzat négyzetes egyenletét nullázzák: ax² + bx + c.

Ebben az esetben x₂| | > | x₁|, akkor a parabola csúcsa középen helyezkedik el. Így a következő kifejezéssel lehet megtalálni: x₀ = ½ (| x₂| | - | x₁|).

Keresse meg az ábra területét

Egy alak területének megkeresése a koordinátántudnod kell az integrálról. És alkalmazzuk, elegendő tudni bizonyos algoritmusokat. Annak érdekében, hogy megtaláljuk a parabola által határolt területet, meg kell adni a képet egy Descartes-koordinátarendszerben.

Először is, a fent leírt módszer szerint aa tengely (x) csúcsának koordinátája, majd a tengely (y), amely után a parabola csúcsát találjuk. Most be kell határoznunk az integráció határait. Általában a probléma állapotában jelennek meg (a) és (b) változók. Ezeket az értékeket az integrál felső és alsó részébe kell helyezni. Ezután írja be a függvény általános értékét, és szorozza meg azt (dx). Parabola esetében: (x²dx.

Aztán általános formában ki kell számítani az antiderivatívata funkció értéke. Ehhez használjon speciális értéktartományt. Az integráció határainak helyettesítése ott van a különbség. Ez a különbség lesz a terület.

Példaként vegyük figyelembe az egyenletek rendszert: y = x₂+1 és x + y = 3.

A metszéspontok abszcisszái vannak: x₁= -2 és x₂= 1.

Feltételezzük, hogy y₂= 3, míg y₁= x² + 1, helyettesíti a fenti képletben szereplő értékeket, és értékét 4,5 értékre állítja.

Most megtanultuk, hogyan találjunk egy parabárt, és ezen adatok alapján számítsuk ki az ábrán szereplő területet, amelyet korlátoz.