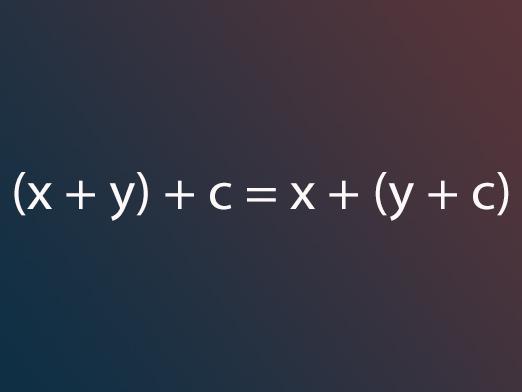Vektorok hozzáadásának szabályai

Annak érdekében, hogy elvégezze a hozzáadás műveletetvektorok, többféleképpen lehet alkalmazni, amelyek a vektorok helyzetétől és típusától függően sokkal kényelmesebbek lehetnek. Nézzük meg a vektorok hozzáadásának szabályait:

A háromszög szabálya

A háromszög szabálya a következő: két x, y vektor hozzáadásához x vektort kell létrehozni úgy, hogy eredete egybeesik az y vektor végeivel. Ezek összege az z vektor értéke lesz, és a z vektor eredete egybeesik az x vektor kezdetével, és a vége az y vektor vége végével.

A háromszög szabály segít abban az esetben, ha a vektorok száma, amelyeket össze kell foglalni, legfeljebb kettő.

Sokszög szabálya

A sokszög szabály a legegyszerűbb és legkényelmesebbbármilyen számú vektor hozzáadásához síkban vagy térben. A szabály lényege a következő: vektorok hozzáadásakor egymás után egymás után egymáshoz kell igazítani őket, úgyhogy a következő vektor kezdete egybeesik az előzővel, és a vektor, amely lezárja a kialakított görbét, a vektorok feltételeinek összege. Ezt grafikusan ábrázolja a w = x + y + z egyenlet, ahol a w vektor e vektorok összege. Ezenkívül meg kell jegyezni, hogy az összeg nem változik a vektorok feltételeinek helyváltoztatásával, azaz (x + y) + z = x + (y + z).

A parallelogram szabály

A párhuzamossági szabály hozzáadásra kerülvektorok, amelyek egyetlen pontból származnak. Ez a szabály kimondja, hogy az összeg a vektorok x és y, amelynek kezdete egy ponton lesz a harmadik vektor Z, származó is ettől a ponttól, és ahol a vektorok x és y jelentése az oldalán a paralelogramma, és a z vektor - a diagonális. Ebben az esetben nem számít, hogy a vektorok milyen sorrendben kerülnek hozzáadásra.

Tehát általánosságban sokszög, általában a háromszög és a paralelogramma segítik, hogy megoldja a problémát a vektor kívül teljesen komplexitás, mind a síkban és a térben.