Hogyan lehet megtalálni a trapéz hegyének szögét?

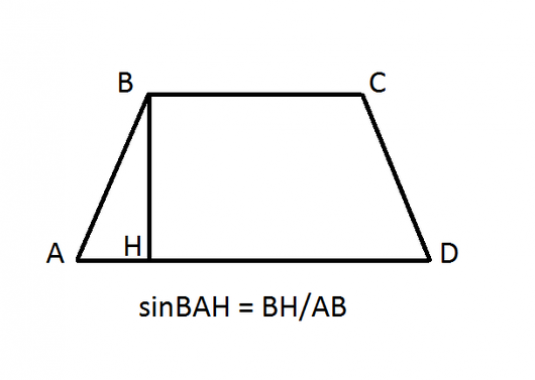
A trapéz négyszög, két oldalán párhuzamos egymással. Tekintsük meg, hogyan találjuk meg a trapéz akut szögének szinuszát, példaként a trapéz ABCD-t használva, ahol az AD és BC oldalak párhuzamosak.

Egy izoelszív trapéz szögének szinuszát keresjük

Vegyünk egy izzűrű trapézet. Az egycsöves trapézban az oldalak egyenlőek. A mi esetünkben AB = CD = 25, és a bázisok mérete AD = 65 és BC = 51. Próbáljuk megtalálni az akut szög szinuszát.

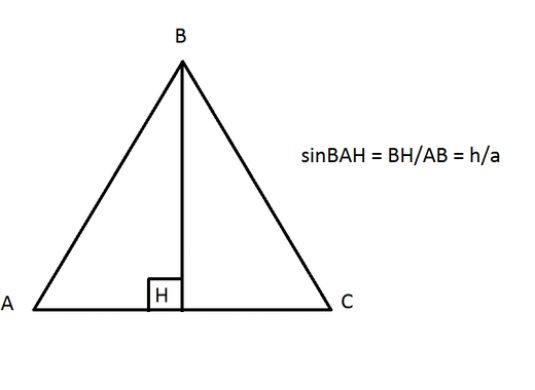
Mint tudják, a szinusz egyenlő az ellentétes láb arányával a hypotenuse-rel, tehát egy jobb háromszögre van szükségünk. Ezt úgy kapjuk, hogy a merőleges BH-t a ABC sarkából az alapra dobjuk.

A trapézis egyik fontos jellemzője a sajátmagasság - a párhuzamos oldalak közötti távolság, amelyet általában bázisnak neveznek. Ennek a távolságnak a meghatározásához le kell meríteni a merőlegeset a másik bázison a kisebb (általában felső) bázis sarkából. A mi esetünkben ezek a VN és a CE merőlegei, amelyekre a szinusz meghatározására van szükség.

A trapéz magasságának meghatározása

Két téglalap alakú háromszöget kapunk, a lábak BH = CE és az AB = CD hipotenisz. Ebből következik, hogy ezeknek a háromszögeknek a többi lába szintén egyenlő az AH = ED értékkel.

Mivel a négyszög NVSE minden sarkából egyenes (HB és CE merőleges a bázis), így kaptunk egy téglalapot, amelynek oldalai BC = CE.

AD = AH + HE + ED építéssel. Mivel AH = ED, és HE = BC, ez az egyenlet a következőképpen írható: