Hogyan lehet megtalálni a parallelepiped térfogatát?

A parallelepipedés a prizma egy speciális változata. Különlegessége abban a tényben rejlik, hogy négyszögletes alakú arcokból áll, és egymás felé néző síkok párhuzamosak. Számos képlet található ennek a számnak a számolásához: egy általános, valamint néhány egyszerűbb módszer, amely a hexaéder adott eseteire alkalmazható.
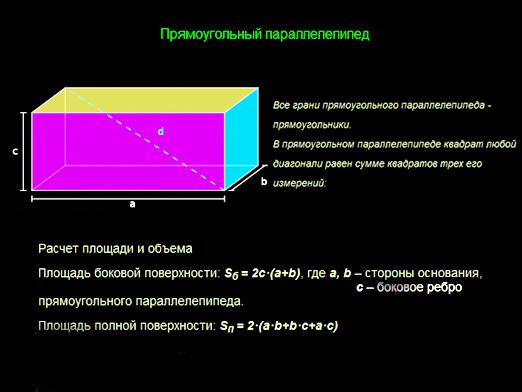
Hogyan lehet megtalálni a parallelepiped térfogatát? Először ki kell számolni a parallelepiped alapja (S) területét. A definíció szerint az egymással ellentétes és a síkot képező oldalak párhuzamosak, a köztük levő szög bármelyik lehet. Ennek megfelelően az arc területe a szomszédos élek (a és b) hosszának a szomszédsága (α) között van: S = a * b * sin (α).
Ezután szorozzuk meg az eredményta parallelepiped (c) szélének hossza, amely szöget képez az a és b oldalakkal. Mivel az oldalsó felület, amelyen ez az él egy rész, nem lehet merőleges az ábrán, akkor a kiszámított értéket meg kell szorozni az oldalsó arcszög (β) szinuszával: V = S * c * sin (β). Összefoglalva, a parallelepiped térfogatának kiszámítására szolgáló képlet így fog kinézni: V = a * b * c * sin (α) * sin (β).
például:
Az ábra alján egy 15. és 25. szélea szög 30 ° között van, az oldalsó felületek 40 ° -os lejtéssel és 20 cm szélességgel rendelkeznek, ilyen méretű térfogat: 15 * 25 * 20 * bűn (30 °) * bűn (40 °) ≈ 7500 * 0, 5 * 0,643 ≈ 2411,25 cm3.
Hogyan lehet megtalálni a négyszögletes párhuzamos tömeget? Ebben az esetben a képlet nagymértékben leegyszerűsödik. A derékszög egyenes szöggel egyenlő, az összes szög a képletet elhagyja, a szomszédos széleknek csak a szimmetrikus széleit kell szaporítani. Az előző példában megadott szélek hosszával a kép térfogata 15 * 25 * 20 = 7500 cm3.