Mi a parallelepiped?

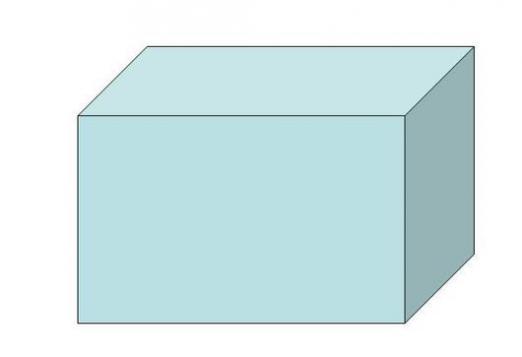
A geometriában a legfontosabb fogalmaksík, pont, vonal és szög. E kifejezések használatával leírhat bármely geometriai ábrát. A polihedrát általában egy egyszerű síkban ábrázolja, pl. Kör, háromszög, négyzet, téglalap, stb. Ebben a cikkben megvizsgáljuk, hogy melyik egy parallelepiped, milyen párhuzamos léptékeket, tulajdonságait, elemeit, valamint az egyes képletek térfogatának és térfogatának kiszámítására szolgáló alap képleteket írja le.

meghatározás

A háromdimenziós térben egy parallelepipedés egy prizma, amelynek mindegyik oldala paralelogramma. Ennek megfelelően csak három pár paralelogramma vagy hat arc lehet.

Képzeld el egy dobozt, képzeld elKépzeljen el egy standard téglát. A tégla egy jó példa a négyszögletes párhuzamos tükörre, amelyet akár egy gyerek is képes elképzelni. Más példák többszintű házak, szekrények, tartályok megfelelő alakú élelmiszertermékek tárolására szolgálhatnak.

Az ábra fajai

A párhuzamos betegségeknek csak két típusa létezik:

Téglalap alakú, amelynek összes oldalsó felülete 90 ° -os szögben van^{körülbelül} az alap és téglalapok.
A függőleges, oldalirányú arcok bizonyos szögben helyezkednek el az alaphoz képest.

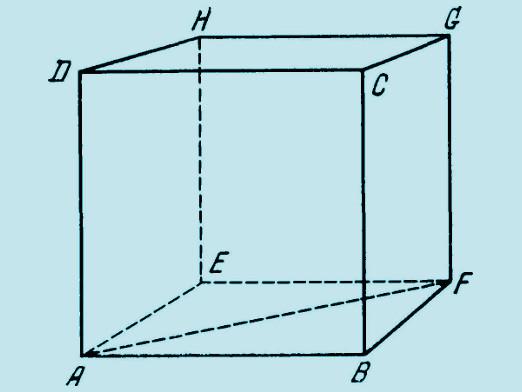
Milyen elemeket lehet felosztani ez a forma?

Mint bármely más geometriai alakban isA párhuzamos párhuzamosan bármelyik két, közös élű arcot szomszédosnak nevezik, és azok, amelyeknek nincsen, párhuzamosak (párhuzamosan párhuzamos párhuzamos oldalú párhuzamosogramok tulajdonságaival).
A párhuzamos körvonalak csúcsait, amelyek nem fekszenek az egyik felületen, ellentétesnek hívják.
Az ilyen csúcsokat összekötő szegmens átlós.
A téglalap alakú parallelepipedék három széleinek egy csúcsra történő összekötése a dimenziója (azaz hosszúsága, szélessége és magassága).

Alak Tulajdonságok

Mindig szimmetrikusan van felépítve a diagonál középen.
Minden átló metszéspontja minden egyes diagonyt két egyenlő szegmensre oszt.
Az ellenkező oldalak egyenlő hosszúságúak és párhuzamos egyenes vonalakon helyezkednek el.
Ha kombinálja a doboz összes dimenziójának négyzetét, az így kapott érték megegyezik az átló hosszának négyzetével.

Számítási képletek

A parallelepiped egyes esetekhez tartozó formuláknak megvan a sajátjuk.

Az önkényes parallelepipedés igazhogy mennyisége megegyezik az egyik csúcsból származó, három oldalú vektorok hármas skaláris termékének abszolút értékével. Az önkényes parallelepipedus térfogatának kiszámításához azonban nincs képlet.

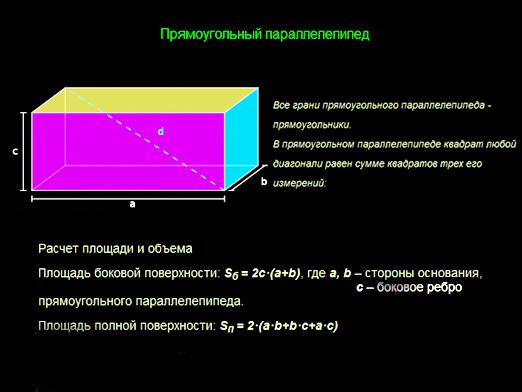
Téglalap alakú parallelepiped esetében a következő képletek alkalmazandók:

V = a * b * c;
Sb = 2 * c * (a + b);
Sn = 2 * (a * b + b * c + a * c).

ahol:

V az ábra térfogata;
Sb az oldalfelület területe;
Sn a teljes felület;
a a hosszúság;
b a szélesség;
c - magasság.

Egy másik, egy parallelepipedus esetében, aamely minden oldal négyzet, a kocka. Ha a négyzet egyik oldalát az a jelzés jelöli, akkor az adott ábra felületi területére és térfogatára a következő képletek használhatók:

S = 6 * a * 2;
V = 3 * a.

ahol:

S az ábra területe,
V az ábra mennyisége,
a az ábra arca hossza.

Az utolsó fajta, amit fontolgatunkA doboz - jobb hasáb. Mi a különbség a közvetlen és a téglatest paralelepipedonja, kérdezed. Az a tény, hogy az alapján a téglatest alakú lehet bármely paralelogramma, és ennek alapján a közvetlen - csak egy téglalapot. Ha jelöljük a kerülete a bázis egyenlő a hosszúságok összegét a minden oldalról, mint a Po, és a magassága betűvel jelöljük H, felhasználhatjuk a következő képletet a térfogat és terület a teljes, és az oldalsó felületek: