Hogyan találhatod meg a doboz magasságát?

Annak érdekében, hogy megtudhassuk, hogyan találjuk meg a párhuzamos kerék magasságát, először meg fogjuk érteni a fogalmakat.

Definíciók:

A parallelepipedés egy hat oldalú poliéder, amelyek mindegyike paralelogramma.

• A párnázott párnák ferde vagy egyenes lehet.
• A ferde párhuzamos párkány egy párhuzamos kör alakú, amelyben az arc nem merőleges az alapra.
• A négyszögletes párhuzamos párkány egy speciális eset, amikor az ábrán minden arc nem csak párhuzamos, hanem téglalap, és merőleges az alapra.
• A parallelepiped magassága a két ellentétes sík közötti távolság (a bázisokhoz merőleges szegmens).

Vegyük fontolóra a párhuzamos kerék magasságának megkeresését.

Megoldás:

Jelölje meg a magasságot h betűvel.

1. módszer: A bázis térfogata és területe megadva

képlet: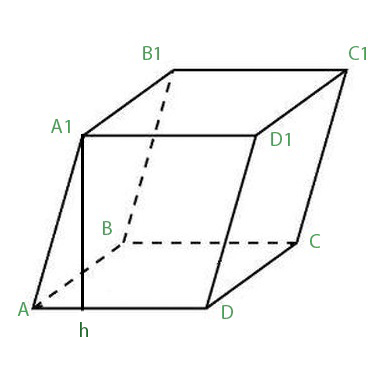

• h = V / S
• Ahol V a doboz térfogata
• S az a terület, amelyre a magasságot húzzuk.

például:

A ferde, párhuzamos ABCDA térfogata₁B₁C₁D₁ 36 cm³, az ABCD bázis területe, amelyhez a magasság 9 cm². Keresse meg a magasságot.

megoldás:

• h = 36/9 = 4 (cm)
• Válasz: 4 cm.

2. módszer: az arcok térfogata és hossza megadva

például:

ABCDA parallelepiped térfogat₁B₁C₁D₁ 36 cm³, az abszolút ABCD hossza, amelyre a magasságot húzta, 4 cm, a szélessége 3 cm.

megoldás:

A magasság képlete változatlan marad:

• h = V / S

S a bázis területe, és a következő képlet segítségével találjuk meg:

• S = a * b,

ahol a és b a paralelogramma oldala, esetünkben AB és BC. Ebből kiindulva megváltoztathatjuk a képlet formáját, az S helyettesítve a * b kifejezést

A következő képletet kapjuk: h = V / (a ​​* b)

A számokat helyettesítjük:

• h = 36 / (3 * 4) = 36/12 = 3 (cm)
• Válasz: 3 cm

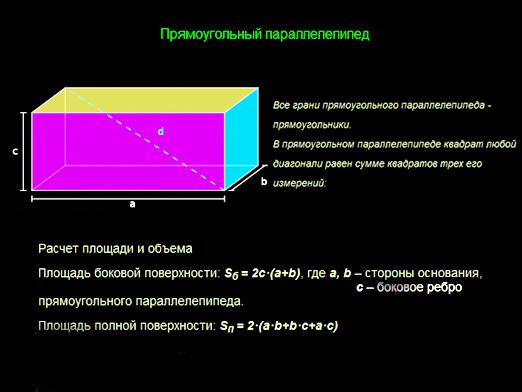
3. módszer: téglalap alakú parallelepiped

Amint azt már kifejtettük, egy ilyen párhuzamos körzet különleges eset. Hogyan lehet megtalálni a négyszögletes párhuzamos kerék magasságát? Nagyon egyszerű - a magasság mindig egybeesik

az egyik oldalon. Ezért, megtalálni, nincs szükség különleges képletekre. Itt kell képleteket találni az arcok hosszát. Például a parallelepiped térfogati képlet:

• V = a * b * c, ahol a, b és c az ábra arcai.

Az arcok bármelyikét a következő képlet adja meg:

• a = V / (b * c), és mivel h ebben az esetben egyenlő a, akkor
• h = V / (b * c)