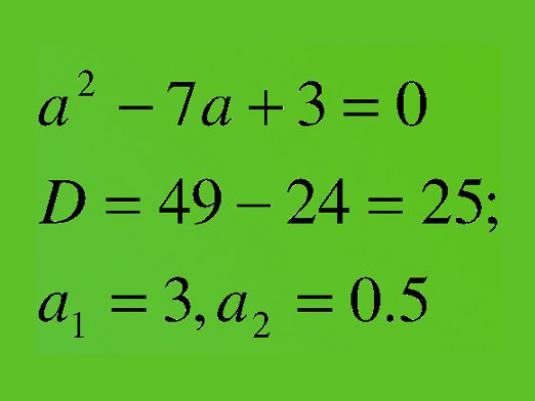Mi az egyenlet?

Azok, akik az algebrában az első lépéseket megteszik,az anyag rendes szállítása szükséges. Ezért cikkünkben, hogy egy ilyen egyenlet, akkor nemcsak definíciót adunk, hanem példákat adunk az egyenletek különböző osztályozására.

Mi az egyenlet: általános fogalmak

Tehát az egyenlet egyfajta egyenlőségismeretlen, latin betűvel jelezve. Ebben az esetben ennek a betűnek a számszerű értéke, amely lehetővé teszi a megfelelő egyenlőség megszerzését, az egyenlet gyökerének nevezzük, és további részleteket olvashat a cikkünkben: Mi az egyenlet gyökere, folytatjuk a beszélgetést az egyenletekről. Az egyenlet (vagy változók) argumentumait ismeretlennek nevezzük, és az egyenlet megoldása az összes gyökere vagy gyökereinek hiánya.

Az egyenletek típusai

Az egyenletek két nagy csoportra oszthatók: algebrai és transzcendentális.

• Az algebrai egy ilyen egyenletamely az egyenlet gyökerének megkeresésére csak algebrai akciókat - 4 aritmetikát, valamint a hatalomra való felemelést és a természetes gyökér kinyerését jelenti.
• Az egyenletet transzcendentálisnak nevezzük, amelyben nem algebrai függvényeket használunk a gyökér megtalálásához: például trigonometrikus függvények, logaritmikus függvények és mások.

Az algebrai egyenletek között megkülönböztetünk továbbá:

• egész - mindkét résznél, amely az ismeretlen algebrai kifejezésekből áll;
• frakcionált - teljes algebrai kifejezések a számlálóban és a nevezőben;
• Az irracionális - algebrai kifejezések a gyökér jelei alatt vannak.

Azt is megjegyezzük, hogy a frakcionális és az irracionális egyenletek csökkenthetők az egész egyenletek megoldására.

A transzcendentális egyenleteket a következőkre osztják:

• Indikatív - ezek az egyenletek, hogytartalmaz egy változót az exponensben. Ezeket úgy oldják meg, hogy egyetlen alapra vagy exponensre költöznek, egy közös szorzót a zárójelek, a faktorálás és más módszerek segítségével;
• Logaritmikus egyenletek logaritmusokkalvannak olyan egyenletek, ahol az ismeretlenek maguk a logaritmusok belsejében vannak. Nagyon nehéz megoldani ezeket az egyenleteket (ellentétben például a legtöbb algebraiakkal), mivel ez szilárd matematikai előállítást igényel. A legfontosabb itt az, hogy az egyenletből a logaritmussal az egyenlet nélkül menjünk, azaz egyszerűsítsük az egyenletet (a logaritmusok törlésének ezt a módját potentiációnak nevezzük). Természetesen csak akkor lehet potenciálálni a logaritmikus egyenletet, ha azonos számbázissal rendelkeznek, és nincsenek koefficiensük;
• Trigonometrikusak a trigonometrikus függvények alatt lévő változók. Megoldásuk megkívánja a trigonometrikus függvények elsajátítását;
• vegyes - ezek differenciált egyenletek a különböző típusú elemekkel (például parabolikus és elliptikus részekkel vagy elliptikus és hiperbolikus stb.).

Ami az ismeretlenek számát illeti,akkor minden egyszerű: megkülönbözteti az egyenleteket egy, kettő, három, és így ismeretlen. Van egy másik osztályozás is, amely a polinom bal oldalán létező fokon alapul. Ebből kiindulva lineáris, négyzetes és köbös egyenleteket különböztetünk meg. A lineáris egyenleteket az 1-fokozatú, a négyzet-2-es és a köbméterek, illetve a harmadikok egyenleteinek is nevezhetjük. Nos, most példákat adunk egy adott csoport egyenleteire.

Példák különböző típusú egyenletekre

Példák az algebrai egyenletekre:

• ax + b = 0
• fejsze³+ bx²+ cx + d = 0
• fejsze⁴+ bx³+ cx²+ bx + a = 0
  (a nem 0)

Példák a transzcendentális egyenletekre:

• cos x = x lg x = x-5 2^x= lgx + x⁵40

Példák az egész egyenletekre:

• (2x + x) 2 = (2 + x) (55x-4) (x2-12x + 10) 4 = (3x + 10) 4 (4x2 + 3x-

Példa a frakcionális egyenletekre:

• 15 x + - = 5x - 17 x

Az irracionális egyenletek példája:

• √2kf (x) = g (x)

Lineáris egyenletek példái:

• 2x + 7 = 0 x - 3 = 2 - 4x 2x + 3 = 5x + 5 - 3x - 2

Négyzetes egyenletek példái:

• x²+ 5x-7 = 0 3x²+ 5x-7 = 0 11x²-7x + 3 = 0

Példák a köbös egyenletekre:

• x³-9x²-46x + 120 = 0 x³- 4x²+ x + 6 = 0

Példák az exponenciális egyenletekre:

• 5^{x + 2}= 125 3^x· 2^x= 8^{x + 3} 3²+ 4 · 3^x-5 = 0

Példák logaritmikus egyenletekre:

• log₂x = 3 napló₃x = -1

Példák a trigonometriai egyenletekre:

• 3sin²x + 4sin x cosx + cos²x = 2 sin (5x + π / 4) = ctg (2x-π / 3) sinx + cos²x + tg³x = ctg⁴x

Példák a vegyes egyenletekre:

• log_x(log₉(4⋅3^x-3)) = 1 | 5x-8 | + | 2⋅5x + 3 | = 13

Ehhez hozzá kell adni, hogy az egyenletek megoldásáraa különböző típusok különböző módszereket alkalmaznak. Nos, szinte bármely egyenlet megoldása érdekében nemcsak az algebra, hanem a trigonometria is szükség lesz, és a tudás gyakran nagyon mély.